¿Qué es la Teoría del Caos?
La teoría del caos es un área de estudio en matemáticas, aunque también se aplica en varias disciplinas como la física, la ingeniería, la economía, la biología, y la meteorología. Se ocupa de los sistemas dinámicos que son muy sensibles a las condiciones iniciales, un fenómeno popularmente conocido como el «efecto mariposa», descrito por la idea de que el aleteo de una mariposa en Brasil podría provocar un tornado en Texas.
Principios fundamentales de la teoría del caos
- Sensibilidad a las condiciones iniciales. Pequeñas variaciones en las condiciones iniciales de un sistema pueden llevar a resultados enormemente diferentes. Esto hace que la predicción a largo plazo sea casi imposible en algunos sistemas caóticos.
- Comportamiento determinista pero impredecible. Los sistemas caóticos son deterministas, lo que significa que su comportamiento futuro es completamente determinado por sus condiciones iniciales, sin necesidad de intervención aleatoria. Sin embargo, debido a la sensibilidad a las condiciones iniciales, estos son prácticamente impredecibles a largo plazo.
- Atractores extraños. Muchos sistemas caóticos tienden a evolucionar hacia un «atractor extraño», que es un conjunto de valores en el espacio de fase hacia el cual el sistema tiende a evolucionar, pero de una manera no repetitiva ni periódica. El atractor extraño tiene una estructura fractal.
- Mezcla topológica. La propiedad de mezcla en los sistemas caóticos implica que las trayectorias del sistema pueden ser extensivamente entremezcladas en el espacio de fase.
Origen y Desarrollo de la Teoría del Caos
La teoría del caos, tal como la entendemos hoy en día, no fue el resultado del trabajo de un único científico, sino más bien el producto de contribuciones de varios expertos en diferentes campos a lo largo del tiempo. Sin embargo, algunos individuos clave jugaron roles fundamentales en su desarrollo y formulación:
- Henri Poincaré (1854-1912). Considerado uno de los padres del estudio del caos, Poincaré fue un matemático francés que hizo contribuciones fundamentales al análisis de la estabilidad del sistema solar y los sistemas dinámicos en general. Descubrió que incluso sistemas con unas pocas partes podrían exhibir comportamientos erráticos y no periódicos debido a la sensibilidad a las condiciones iniciales.
- Edward Lorenz (1917-2008). Meteorólogo y matemático estadounidense, Lorenz es quizás el más directamente asociado con el desarrollo moderno de la teoría del caos. En 1963, publicó un artículo en el que describía lo que luego se llamaría el «atractor de Lorenz», encontrando que pequeñas diferencias en las condiciones iniciales de un modelo atmosférico podían generar trayectorias completamente divergentes. Este fenómeno fue popularizado como el «efecto mariposa», que Lorenz describió con la pregunta retórica: «¿Puede el aleteo de una mariposa en Brasil provocar un tornado en Texas?».
- Mitchell Feigenbaum (1944-2019). Físico estadounidense que descubrió las constantes universales que caracterizan el comportamiento de los sistemas dinámicos que se vuelven caóticos a través de periodos de duplicación. Su trabajo ayudó a proporcionar una estructura matemática para entender cómo diferentes sistemas dinámicos pueden exhibir transiciones al caos de manera similar.
- James Yorke (nacido en 1941) y T. Y. Li. Co-acuñaron el término «caos» en un artículo científico de 1975 que llevó este campo de estudio al reconocimiento mainstream. Su trabajo mostró cómo sistemas con reglas deterministas simples podían resultar en comportamientos dinámicos complejos y aparentemente aleatorios.
Aplicaciones de la teoría del caos
- Meteorología. Quizás el ejemplo más famoso de caos es el pronóstico del tiempo, donde pequeños errores en las mediciones de las condiciones atmosféricas pueden crecer exponencialmente, haciendo que los pronósticos a largo plazo sean muy inciertos.
- Biología. Se utiliza para modelar la dinámica de las poblaciones biológicas y para entender fenómenos como las epidemias.
- Economía. Ayuda a modelar los mercados financieros y otros sistemas económicos que exhiben comportamientos impredecibles.
- Física. En sistemas de partículas, turbulencia y otros fenómenos físicos complejos.
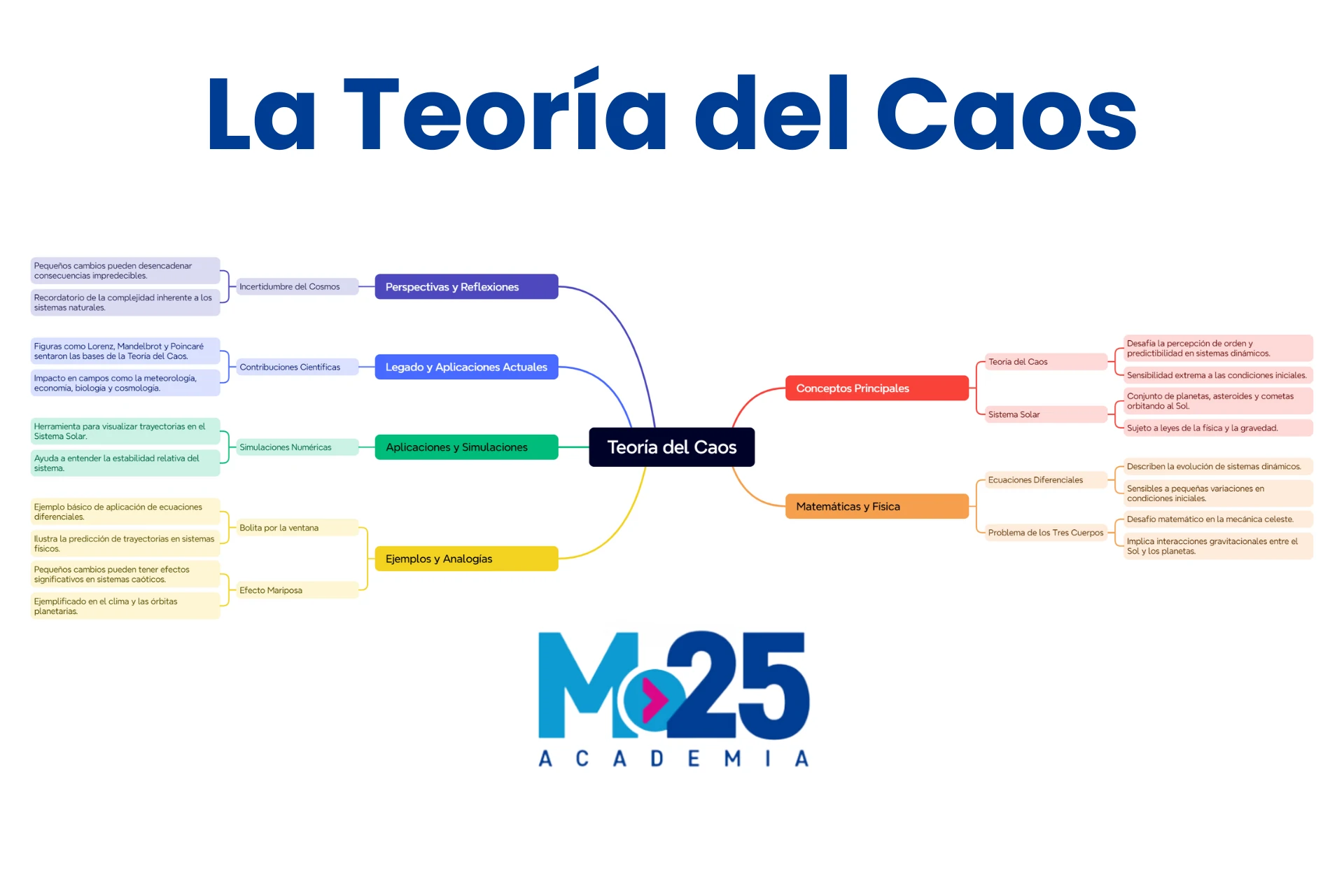
Mapa conceptual de la Teoría del Caos
Ejemplos y analogías de la Teoría del Caos
Efecto Mariposa
El «efecto mariposa» es un concepto popular dentro de la teoría del caos que ilustra cómo pequeñas variaciones en las condiciones iniciales de un sistema dinámico pueden tener grandes y amplias consecuencias a largo plazo. Este término fue popularizado por Edward Lorenz, quien lo descubrió mientras trabajaba en modelos climáticos. La metáfora del efecto mariposa se explica a menudo con la frase: «El aleteo de las alas de una mariposa en Brasil podría desencadenar un tornado en Texas».
Fundamentos del Efecto Mariposa
- Sensibilidad a las condiciones iniciales. Este es el aspecto clave del efecto mariposa y de la teoría del caos en general. Incluso diferencias minúsculas en el estado inicial de un sistema pueden llevar a resultados enormemente diferentes, lo que hace que la predicción a largo plazo sea extremadamente difícil o imposible en sistemas complejos.
- Implicaciones. Este efecto tiene profundas implicaciones en diversas áreas como la meteorología, la economía, la física, y más. En la práctica, significa que algunos sistemas son inherentemente impredecibles después de un cierto punto temporal.
Problema de los Tres Cuerpos
El problema de los tres cuerpos es un famoso problema en mecánica celeste que trata de determinar el movimiento de tres cuerpos celestes que interactúan gravitacionalmente entre sí de manera exacta y general. Originado en el siglo XVII con Isaac Newton, ha sido un desafío constante en la astronomía y la física.
Características del Problema de los Tres Cuerpos
- Complejidad. A diferencia del problema de dos cuerpos, que tiene soluciones precisas y bien definidas, el problema de tres cuerpos (sin restricciones específicas) no tiene una solución general que pueda ser expresada en términos de funciones elementales.
- Soluciones numéricas y especiales. Mientras que no existe una solución general, existen soluciones para casos especiales (como el problema restringido de los tres cuerpos) y se pueden obtener aproximaciones mediante métodos numéricos.
- Caos. El sistema de tres cuerpos puede exhibir comportamiento caótico, especialmente en configuraciones donde los cuerpos están en proximidad relativamente cercana y tienen masas comparables. Esto significa que pequeñas diferencias en las condiciones iniciales pueden llevar a divergencias significativas en la evolución del sistema, vinculando este problema con el efecto mariposa en el contexto de la dinámica del sistema.
Conoce en nuestra página más recursos y ejercicios gratuitos.